We have submitted a new contribution

A Comparison of a Minimization and a Saddle Point Formulation of a Coupled Mechanics-Diffusion Problem Implemented in deal.II; Akshay Balachandran Jeeja, Bjoern Kiefer, Stefan Prüger, Oliver Rheinbach, and Friederike Röver (2024)

Formulation matters, discretization matters

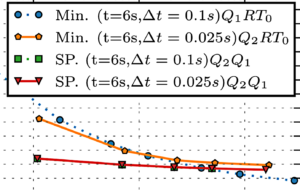
We consider the mechanically induced diffusion in a hydrogel, using a minimization formulation („Min.“), using Q₁RT₀ and Q₂RT₀ finite elements, and a saddle point formulation („SP“), using Q₂Q₁ finite elements.

In our context, we discard the Q₁RT₀ discretization for the minimization formulation as it seems to converge to a different limit for our quantity of interest than all the other discretizations; see the blue circles in the figure.

Comparing the saddle point formulation (SP) using a Q₂Q₁ discretization with the minimation problem (Min.) using Q2RT0, both, for a time step of 0.025, the quality of interest seems to converge much earlier for the saddle point formulation, i.e., using fewer finite elements. Moreover, for the saddle point formulation the larger time step 0.1 gives the same results (up to four digits) as the finer time step 0.025. However, for the minimization formulation using Q₂RT₀ all computations failed due to distorted elements for the larger time step of 0.1. Here, clearly, being able to use a larger time step is a significant advantage of the SP formulation with Q₂Q₁. Note, however, if larger problems are considered, the large time step will fail also for the SP formulation with Q₂Q₁ and a time step of 0.1 due to the singularity caused by the boundary conditions. Thus a smaller time step is then also needed.

Let us we consider cases with roughly the same problem size for SP with Q₂Q₁ and Min. with Q₂RT₀, both, for a time step of 0.025. Here, we observe that fewer Newton steps are need in the SP formulation. Although the finite element assembly is slower for the SP formulation, in the end it is faster by a factor of 1.4.

However, the saddle point formulation is faster by a factor of more than 5 if a time step of 0.1 is used, which gives the same results, up to four digits, as the finer time step of 0.025.

The CoDes -project is happy to announce a Workshop  „Parallel Simulation with MPI, Trilinos and FROSch“ (Sept. 2nd to 4th 2024) at the Technische Universität Bergakademie Freiberg, Freiberg, Germany.

Further details can be found  here.

CoDes is part of the DFG SPP2256.

CoDes has announced a workshop on „Parallel Simulation with MPI, Trilinos and FROSch“ (Sept. 02-04, 2024) in Freiberg, Germany.

Project publikations acknowledging the SPP2256

• Akshay Balachandran Jeeja, Bjoern Kiefer, Stefan Prüger, Oliver Rheinbach, and Friederike Röver, A Comparison of a Minimization and a Saddle Point Formulation of a Coupled Mechanics-Diffusion Problem Implemented in deal.II (submitted 06/2024).
  
• Heinlein, Alexander, Rheinbach, Oliver and Röver, Friederike. „A Multilevel Extension of the GDSW Overlapping Schwarz Preconditioner in Two Dimensions“, Computational Methods in Applied Mathematics, vol. 23, no. 4, 2023, pp. 953-968. https://doi.org/10.1515/cmam-2022-0168
• Kiefer, B., S. Prüger, Rheinbach, O., and F. Röver. „Monolithic Parallel Overlapping Schwarz Methods in Fully-Coupled Nonlinear Chemo-Mechanics Problems“. In: Comput Mech 71, 765–788 (2023). https://doi.org/10.1007/s00466-022-02254-y .
• A. Heinlein, Rheinbach, O., and F. Röver. „Parallel Scalability of Three-Level FROSch Preconditioners to 220000 Cores using the Theta Supercomputer“. In: SIAM J Sci Comput 0.0 (0). 2022. First available online, S173–S198.  https://dx.doi.org/10.1137/21M1431205 .
• A. Heinlein, A. Klawonn, Rheinbach, O., and F. Röver. „A Three-Level Extension for Fast and Robust Overlapping Schwarz (FROSch) Preconditioners with Reduced Dimensional Coarse Space“. In: Springer series: Domain Decomposition Methods in Science and Engineering XXVI.
  Proc. 26th Internat. Conf. on Domain Decomposition Methods, Hong Kong. Ed. by S. Brenner, E. Chung, A. Klawonn, F. Kwok, J. Xu, and J. Zou (2023). URL: http://www.ddm.org/DD26/proceedings/475.pdf . Also: http://dx.doi.org/10.13140/RG.2.2.18009.03681 .
• A. Heinlein, O.Rheinbach, and F. Röver. „Choosing the Subregions in Three-Level FROSch Preconditioners“. In: Proceedings of the WCCM-ECCOMAS2020; Virtual Congress: 11-15 January 2021. http://dx.doi.org/10.23967/wccm-eccomas.2020.084 .
• Kiefer, B., Rheinbach, O., S. Roth, and F. Röver. „Variational Methods and Parallel Solvers in Chemo-Mechanics“. In: Proc Appl Math Mech 20.1 (2020), e202000272. https://dx.doi.org/10.1002/pamm.202000272 .
• Kiefer, B., S. Prüger, Rheinbach, O., F. Röver, and S. Roth. „Variational Settings and Domain Decomposition Based Solution Schemes for a Coupled Deformation-Diffusion Problem“. In: Proc Appl Math Mech 21.1 (2021), e202100163. https://dx.doi.org/10.1002/pamm.202100163 .