Um Entscheidungen zu Epidemien zu treffen (oder zu verstehen) muss man zuerst exponentielles Wachstum verstehen: aus 100 Infizierten werden schon nach 20 Verdopplungen 100 Millionen Infizierte.
Dieses explosive Wachstum führt dazu, dass Krankenhäuser überlastet werden. Um die Geschwindigkeit des Wachstums zu reduzieren, kam es in fast allen Ländern der Welt mit exponentiell schnellen Ausbrüchen zu radikalen Maßnahmen, wie etwa die Kontaktbeschränkungen (+weiteren Maßnahmen) in Deutschland. Einige Länder kamen ohne solche Maßnahme aus, weil Sie den jeden Ausbruch früh genug unter Kontrolle bekommen haben. Italien, Frankreich und Spanien hatten dagegen deutlich strengere Maßnahmen als Deutschland (d.h. echte Ausgangssperren), mit ähnlichem Erfolg wie Deutschland.
Exponentielles Wachstum tritt am Anfang einer Epidemie auf. Durch erworbene Immunität schwächt sich die Epidemie ab, sobald ein substantieller Anteil der Bevölkerung die Infektion durchgemacht hat.
Die einfachsten Modelle, die dieses Verhalten beschreiben, sind die schon erwähnten SIR-Modelle und verfeinerte Varianten davon. Solche Modelle sind nötig, um Fragen zu beantworten wie: Wie hoch wird die Zahl der gleichzeitig Infizierten maximal sein und wann wird das sein? Wie hoch wird der Anteil der Bevölkerung sein, der sich im schlimmsten Fall ansteckt? Auch das RKI verwendet Varianten von SIR-Modellen für Grippesimulationen und jetzt auch für SARS-CoV-2.
Es gibt ein paar Online-Rechner zu SIR-Modellen, zum Teil mit sehr vielen Parametern. Das einfachste Modell kommt jedoch mit zwei Parametern aus: alpha und beta. Die sogenannte Basisreproduktionszahl R0, über die zur Zeit so viel diskutiert wird, ist dann der Quotient beta/alpha.
Das Modell hat nur drei Variablen:
- S (susceptibles; Ansteckbare)
- I (infected; Infizierte)
- R (recovered/removed; Geheilte oder Verstorbene)
Die Werte der Variablen liegen immer zwischen 0 und 1, was sich dann als 0 Prozent bis 100 Prozent der Bevölkerung interpretieren lässt.
Das SIR-Modell wird durch ein System gewöhnlicher Differentialgleichungen beschrieben (vielleicht folgt in einem weiteren Beitrag die diskretisierte Variante, die dann ohne sichtbare Ableitung auskommt), in der einfachsten Variante:
- S'(t)=-beta*S(t)*I(t)
- I'(t)=beta*S(t)*I(t) – alpha*I(t)
- R'(t)=alpha*I(t)
Hier gibt die Konstante beta an, wieviele andere ein Infizierter pro Zeiteinheit (z.B. pro Tag) ansteckt. Aus I(t) Infizierten (z.B. 10 Prozent der Bevölkerung) werden also nach einem Tag beta*I(t) Infizierte (also z.B. 15 Prozen, wenn beta=3/2), sofern jeder infizierbar ist. Da aber nur S(t) infizierbar ist (90 Prozent sind noch infizierbar, weil 10 Prozent ja schon infiziert sind), wird noch mit S(t) multipliziert.
Die mittlere Gleichung sagt also: Pro Tag kommen beta*S(t)*I(t) Infizierte dazu (immer in Prozent gerechnet, da alle Variablen zwischen 0 und 1 sind).
Die erste Gleichung sagt, dass die Anzahl der Infizierbaren entsprechend sinkt.
Die letzte Gleichung sagt, dass pro Zeiteinheit (z.B. pro Tag) ein Anteil alpha der Infizierten gesundet (oder stirbt, das wird hier nicht unterschieden). Daher ist 1/alpha ist die durchschnittliche Krankheitsdauer (z.B. 7 Tage).
Wenn beta die Infektionen pro Tag sind und 1/alpha die Krankheitsdauer in Tagen, dann sind beta/alpha die Infektionen, die ein Kranker während seiner gesamten Krankheit verursacht (wenn niemand immun oder bereits infiziert ist). Das ist die Basisreproduktionszahl R0.
Das Modell weicht natürlich von der Realität der SARS-CoV-2-Epidemie ab. Beispiel: Ein Infizierter ist im Modell während seiner Krankheit jeden Tag gleich ansteckend. Bei SARS-CoV-2 ist es so, dass ein Infizierter in den ersten Tagen nach seiner eigenen Infektion besonders ansteckend ist (mit einem Höhepunkt am Tag unmittelbar vor dem Symptombeginn), obwohl er noch keine Symptome hat (im Median 5 Tage lang). In der zweiten Woche ist ein Infizierter kaum mehr ansteckend (außer bei engem Kontakt z.B. mit Krankenhauspersonal) – obwohl er sich dann erst richtig krank fühlt.
Aus diesem Grund wollen wir für unser Modell 1/alpha = 7 Tage Krankheitsdauer annehmen. Das heißt, wir nehmen an, dass alle Ansteckungen während der ersten 7 Tage passiert (und ignorieren die zweite Krankheitswoche des durchschnittlichen Covid-19-Patienten).
Wenn wir nun versuchen, beta so zu wählen, dass es auf die SARS-CoV-2-Infektionsdaten in Deutschland vom Anfang März 2020 passt, bekommen wir den folgenden Verlauf (S blau, I rot, R grün). Tag 0 ist wieder der 1. März 2020. Die genauen Parameter sind beta=2.85/7 und alpha=1/7. Dementsprechend ist R0=2.85, also knapp unter 3. Das passt grob zur (rückwärts berechneten) Schätzung des RKI von R0 für Anfang März 2020 und zu anderen Quellen.
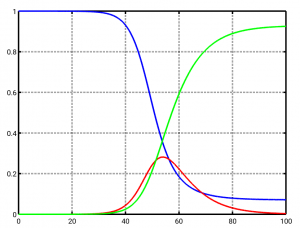
Dieses Szenario beschreibt, was passiert wäre, hätte es gar keine eindämmenden Maßnahmen gegeben – für diesen Fall ist dieses einfache Modell sogar relativ gut geeignet. Man sieht, dass kurz nach Tag 50 (genauer: am Tag 54, das wäre der 23. April 2020 gewesen, also vorgestern) das Maximum bei den Infizierten erreicht wird (rote Kurve): Es sind an diesem Tag fast 30 Prozent (genauer: 28 Prozent) der Bevölkerung gleichzeitig infiziert. Eine Katastrophe für die Krankenhäuser, denn selbst wenn nur ein Prozent schwere Verläufe angenommen werden, bedeutet das über 200000 Schwerkranke (bei aktuell 30000 Intensivbetten in Deutschland, von denen maximal 2/3 für Covid-19 zur Verfügung stehen werden.)
Ingesamt werden innerhalb der 100 Tage Berechnungszeit über 90 Prozent der Bevölkerung infiziert (grüne Kurve).
Ich habe oben geschrieben, dass beta=2.85/7 (bei angenommenen alpha=1/7, also 7 Tage Erkrankungsdauer) so gewählt wurde, dass es zu den deutschen Daten von Anfang März passt. Hier ist dargestellt, wie gut es passt:
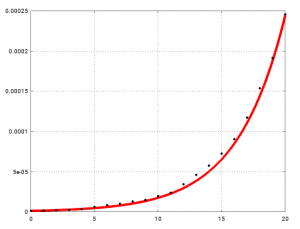
Der Vergleich von I(t) (rote Kurve) mit den Infektionszahlen (Daten von NTV, siehe den allerersten Blog-Beitrag) geteilt durch 80 Millionen (schwarze Punkte). Die Kurve passt gut.
Hier die Messwerte (schwarze Punkte) noch einmal, aber eingetragen ein einen semilogarithmischen Plot von S, I und R (in der Standarddarstellung wie oben, könnte man nichts zu erkennen).
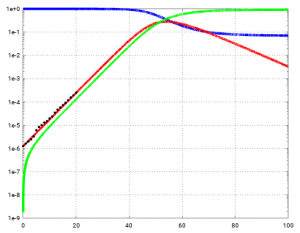
Man sieht, dass die rote Kurve sehr gut zu den Infektionszahlen in Deutschland (1. März bis 21. März 2020) passt. Da die y-Achse logarithmsch aufgetragen ist (semilog) ist, ist die Phase des exponentiellen Wachstums als Geradenabschnitt zu sehen. Die Steigung passt gut zusammen.
Im ersten Beitrag haben wir gesehen, dass das exponentielle Modell für den Tag 40 etwa 4,4 Millionen Infizierte prognostiziert hat. In der semilogarithmischen Plot (y-Achse logarithmisch) sieht man, dass das exponentielle Modell ungefähr bis Tag 45 gültig ist, hier der Ausschnitt bis Tag 45:
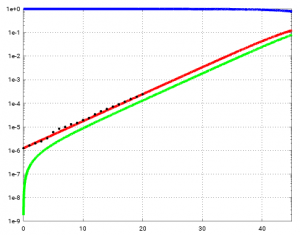
Das bedeutet aber, dass auch dieses Modell (ohne Eindämmungsmaßnahmen) vorhersagt, dass innerhalb von 40 Tagen aus 100 Infizierten mehr als 4 Millionen werden (etwa 5 Prozent der Bevölkerung bzw. 5e-2).
Nach Tag 45 ist die Phase des exponentiellem Wachstum (mit konstantem Wachstumsfaktor) beendet. Allerdings sind nach Tag 46 fast 15 Prozent der Bevölkerung infiziert (entsprechend 12 Mio Infizierten) – erst dann kommt es zu einer sichtbaren Abschwächung des Wachstums.
Bemerkung zu R0: Wenn man aus echten Daten den Wert von R0 schätzen will, muss man immer eine Generationenzeit annehmen. Das RKI berechnet R0 so (S. 14):
Schlussbemerkungen: Wir haben nur zwei Parameter (beta und alpha), dennoch gibt es noch andere Kombinationen von beta und alpha, die ähnlich gut zu den Daten passen. Sie liefern aber auch Ergebnisse, die ähnlich sind.
Eigentlich wollte ich Ihnen Octave-Implementierung (entweder mit Euler oder mit dem eingebautem ODE-Löser) an die Hand geben, damit Sie die Rechnungen nachvollziehen können – das verschieben wir aber.
Korrektur (06.07.2020): In der zweiten Gleichung des (einfachsten) SIR-Modells fehlte „- alpha*I(t)“. Danke für den Hinweis.
Das verwendete SIR-Modell beschreibt sehr anschaulich und präzise das exponentielle Wachstum. Es berücksichtigt allerdings nicht die begrenzten Ressourcen (N ist endlich) wie bei den LogisticCurve-Modellen sondern setzt implizit voraus, dass N unendlich gross ist. Wenn I/S immer grösser wird, muss irgendwann der Fall eintreten, dass es gar nicht mehr genug Individuen in S*I gibt, so dass jeder in I 2,85 in S*I infizieren kann. Könnte man das endliche N nicht durch den folgenden Ansatz auch in das SIR-Modell einbauen, indem man in
I’=(R0*S-1) * I das R0 ersetzt durch eine dynamische Wachstumsrate, z.B.: RZ(I/S)=R0 – (R0-1) * I/S. Der Ansatz ist zumindest plausibel: Bei sehr kleinen I ist RZ=R0 wie bisher, bei I/S=1 ist RZ=1, dI/dt=0 und I(t) bleibt konstant und bei I/S=0,2 würden 80% der Personen aus I 2,85 infizieren und 20% nur einen, da gar nicht mehr genug da sind. Die exponentielle Wachstumsrate würde irgendwann begrenzt, I(t) wird flacher und breiter und das Maximum kleiner, bevor dann irgendwann die Herdenimmunität einsetzt und Reff=RZ * S(t)<1 wird. Vermutlich darf niemals RZ=1 werden, da sonst I(t) in eine Konstante hineinläuft wie bei den Logistic Curve Modellen. Wenn man zusätzlich noch das Impfen mit einer konstanten Impfquote q, die als -q*t das S(t) stetig absenkt bis 1-Impfwilligkeit, könnte man das Ende der Pandemie vielleicht noch exakter vorhersagen. Die Frage ist überhaupt, wie gross N ist: 80Mio. oder 400Mio. ? N klein und Grenzschliessungen sind gut für die Pandemiekontrolle.
Das SIR-Modell ist in der Tat ein kontinuierliches Modell, während die Wirklichkeit diskret ist, d.h. die Bevölkerungszahl N ist endlich. Solange N aber groß ist, ist das kein Problem. Wenn man daran zweifelt oder wenn N klein ist, kann man zu einem diskreten Modell übergehen, wo wirklich jeder einzelne Mensch im Modell repräsentiert ist. Mit heutiger Rechenpower ist das kein Problem. Als die SIR-Modelle entstanden sind, war das noch anders.
1. Wäre es nicht sinnvoller, die Dynamik von vornherein diskret zu formulieren? Damit umgeht man das Problem, dass viele Differentialgleichungen analytisch nicht lösbar sind. Die Dynamik einer Infektionswelle ist schließlich schon deshalb ein diskreter Prozess, weil eine Person nicht weiter geteilt werden kann und kleinere Zeitintervalle, als 1 Tag keinen Sinn machen.
2. Ist es nicht sinnvoller die Reproduktionsrate auf einen Tag zu normieren?
Wenn das serielle Intervall 4 Tage währt und die Basisreproduktionszahl über diese Zeit 3 beträgt, dann beträgt sie auf den Tag bezogen 3^ (1/4)= 1,316
Die resultierende Exponentialfunktion ist die gleiche. I(t+4)=(I(t) *3 oder I(t+1)= I(t) * 1,316
Zu 1.: Man kann das Modell natürlich auch direkt diskret formulieren und das wird auch gemacht. Es ist Geschmackssache. Im Wesentlichen ist es nur die Frage welche Sprache einem näher ist. Und über Differentialgleichungen vom bestimmten Typ weiss man eben so einiges, was man nutzen kann.
Zu 2.: Solange es die Mathematik nicht ändern, kann man es natürlich so umformulieren, wie man es mag.
Hallo Herr Käsmacher,
zwischenzeitlich bekam ich sehr viel Spam, aber nun scheinen Sie einer der letzten zu sein, der sich noch für diese Seite interessiert. Ich arbeite also Ihre Bemerkungen nach und nach ab.
Zu 1. Siehe Antwort oben: Das SIR-Modell ist in der Tat ein kontinuierliches Modell, während die Wirklichkeit diskret ist. Man kann das Modell daher auch direkt diskret formulieren wenn man will. Dann verliert man ein paar Einsichten, die dem Differentialgleichungsmodell einfacher zu entnehmen sind, aber dafür ist das diskrete Modell einfacher verständlich.
Zu 2. Sie können die Reproduktionsrate auf einen Tag beziehen, wenn Sie wollen. In Übungsaufgaben zu dem Thema schreibe ich auch immer dazu, dass die Studierenden als ersten Versuch delta t auf einen Tag setzen sollen. Das ist genau genug, auch wenn ein kleineres delta t etwas genauere Ergebnisse liefert (im Sinne der Approximation der Lösung der Differentialgleichung).
Sie gehen in ihrem Artikel von einer Basisreproduktionszahl von 2,6 aus. Am Maximum der Infektionskurve ist dann die momentan effektive Reproduktionszahl=1. Soweit so gut.
Ich weiß zwar nicht, wie sie nun die die bekannte Formel für die minimale Herdenimmunität aus ihrem Modell abgeleitet haben, aber dieser Formel H=1-1/Ro zufolge , ergibt sich für den angenommenen Ro-Wert von 2,6 pro 4 Tage eine minimale Herdenimmunität von 0,615.
Wäre nun die Infektionskurve symmetrisch, dann betrüge die Immunität der „Herde“ am Ende nach dieser Formel das Doppelte. Da die Kurve asymmetrisch verläuft und daher die Fläche unter dem rechts vom Maximum liegenden Kurvenanteil größer ist, als die linke Hälfte, wäre die Immunität am Ende der Kurve noch größer.
Wie erklären sie diesen Widerspruch? Mehr als 100% der Bevölkerung können nicht immun werden.
Zudem frage ich mich, wie die bekannte Formel die minimale Herdenimmunität wiedergeben soll, wenn jeder die Basisreproduktionszahl auf ein unterschiedlich großes serielles Intervall normiert.
Irgendetwas kann an ihrem Modell nicht stimmen.
Nun, liebe Autoren, wäre es doch angemessen, 4 Monate nach Erscheinen meines Einwandes gegen das SIR-Modell, hier mit wissenschaftlichen Argumenten zumindest zu antworten.
Es sollte nur folgendes feststehen: 1. die Reproduktionsrate hat ohne gleichzeitige Angabe des seriellen Intervalls oder eines anderen definierten Zeitintervalls (z.B. Inkubationszeit) keinerlei Aussagekraft. Eine Normierung auf ein Zeitintervall ist Voraussetzung überhaupt eine numerische Simulation durchführen zu können. Man kann es beliebig klein wählen.
Es dürfte 2. klar sein, dass Simulationen, auch wenn die Modelle stimmig sind lediglich den Verlauf ohne jede Maßnahme beschreiben können. Für jede Massnahme gegen die Ausbreitung müssen hingegen Annahmen getroffen werden und zusätzliche Variable definiert werden, für die es keine empirisch ermittelten Daten gibt. So liegen die Vorhersagen oft 2 Zehnerpotenzen daneben, weil die Modelle nur das berechnen können, was der Programmierer festlegt.
Hallo Herr Käsmacher,
es gibt hier nur einen Autor.
Zu 1.: Korrekt. Wie oben auch im Text steht: „Wenn man aus echten Daten den Wert von R0 schätzen will, muss man immer eine Generationenzeit annehmen.“
Zu 2.: Korrekt. Das einfache SIR-Modell beschreibt den Verlauf ohne Maßnahmen und ohne Verhaltensänderung der Menschen. Nichts anderes wurde behauptet. Es ist eine Worst-Case-Abschätzung, die nur eintritt, wenn die Gesellschaft (im Großen) nicht reagiert und wenn die Einzelpersonen (im Kleinen) nicht reagieren.
Hallo Herr Käsmacher,
die oft (auch von Herrn Drosten, wenn ich mich recht erinnere) erwähnte Formel für die Herdenimmunität ist nur eine Approximation für die Anzahl der Menschen, die sich letzlich infizieren. Die Faustformel ist trotzdem hilfreich, weil man so schnell eine Überschlagsrechnung machen kann.
Sie sehen an der grünen Kurve, wieviel Prozent der Bevölkerung sich in dieser SIR-Rechnung am Ende infizieren: Etwas mehr als 90 Prozent.
Wie im Text erwähnt, braucht man in der Tat immer auch eine Generationenzeit. Das RKI hat zu Vereinfachung immer 4 Tage genommen (siehe oben im Text), auch wenn die „echte“ Generationenzeit (wenn man Sie exakt messen könnte) sicherlich keine ganze Zahl ergäbe.
Die Herdenimmunität ist klar definiert. Sie tritt dann ein, wenn die Reproduktionszahl <=1 wird. Das ist genau beim Maximum der Inzidenzkurve der Fall. Mein Modell liefert genau den nach der Formel H=1-1/R0 errechneten Wert. Wenn ein Herr Drosten der Bevölkerung klar machen will, was Herdenimmunität bedeutet und dazu annimmt, dass ein Infizierter 3 andere ansteckt und zwar innerhalb einer Woche, dann beträgt die Herdenimmunität in diesem Beispiel zwar 66,7%. Der Wert ist aber falsch. Normiert man nämlich die verwendete Basisreproduktionszahl von 3 pro Woche auf einen Tag um, dann ist R0 (pro Tag) =1,17 und die Herdenimmunität tritt bei einer Immunität von 14,5% ein.
Aufgrund dieser falschen Ausführungen Drostens leitete die Politik eine notwendige Durchimpfungsrate von 70% ab.