Der Virologe Christian Drosten weist seit Langem darauf hin, dass Kontakttagebücher und (neben der Vorwärtsverfolgung) die Rückwärtsverfolgung von Kontakten wichtig sind. Sehr interessant ist auch der Artikel auf theatlantic.com zum erfolgreichen Einsatz von Rückwärtsverfolgung in Asien.

Auch jetzt, wo erste Ballungszentren in Deutschland mit den Kontaktnachverfolgung nicht mehr nachkommen (hier Berlin), bleibt dies gültig.

Es geht darum, dass sich SARS-CoV-2 vor allem durch Superspreading-Events verbreitet. Grob gesprochen heisst dies, dass 10 Prozent der Infizierten 80 Prozent der Neuinfektionen verursachen. Im Umkehrschluss bedeutet das, das viele Infizierte niemanden infizieren (wer z.B. vom seinem bereits erkrankten Partner im Haushalt angesteckt wurde, wird wahrscheinlich niemand weiteren mehr anstecken, sondern von Anfang an mit dem Partner zuhause geblieben sein; sehr wahrscheinlich ist man sogar früh genug in angeordneter Quarantäne).

Dies ist die mathematische Arbeit zum Thema Rückwärtsverfolgung, die im Artikel in „The Atlantic“ erwähnt wird. Der Artikel ist unter eine Creative-Common-Lizenz (CC BY 4.0) publiziert, weshalb ich hier die wichtigste Abbildung darstellen kann.

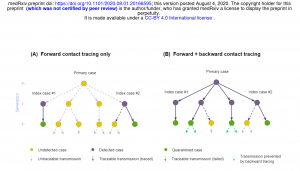
Die Botschaft ist:

Wurde ein Corona-Infizierter gefunden, wird er über seine Kontakte befragt. Bekanntermaßen ist ein Infizierter bereits ca. 4 Tage vor den ersten Symptomen infektiös. Daher müssen alle Risikokontakte bis vor Tage vor Symptombeginn gesucht werden.

Da sich SARS-CoV-2 vor allem durch Superspreading-Events verbreitet, findet man bei der Vorwärtssuche einige wenige Risikokontakte. Schaut man aber rückwärts (stellt man also die Frage, wo die Person sich angesteckt hat), findet man mit großer Wahrscheinlichkeit ein Superspreading-Event (daher müssen Gesundheitsämter unbedingt nach Feiern, Gottesdiensten, etc. fragen). Die Teilnehmer an diesem Event müssen dann alle sofort (ohne Test) unter Quarantäne gestellt werden. Im nächsten Schritt müssen deren Kontakte ebenfalls gesucht werden (siehe Abbildung oben).

Hier noch ein Beispiel mit 5 Infizierten (oberste Reihe, genannt A1 bis A5). Es wird angenommen, dass jeder Infizierte durchschnittlich 2 weitere Personen mit Corona infiziert. Allerdings erfolgt die Übertragung hauptsächlich durch durch Superspreader. Hier steckt A1 insgesamt 8 weitere an (B1 bis B8), A2 und A3 stecken niemanden an und A4 und A5 jeweils eine Person (B9 und B10).

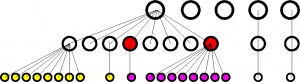
Dieses Verhalten setzt sich in der nächsten Generation fort: B1 steckt 8 Personen an, B8 ebenfalls 8 Personen; B3, B4, B9 und B10 stecken eine Person ab. Angenommen B4 und B8 werden durch Tests zufällig entdeckt, weil sie sich nach Symptomen in einem Testzentrum vorgestellt haben. Sie haben jedoch bereits andere angesteckt (Infektionsität beginnt ca. 4 Tage vor Symptomen).

Wird nun nur vorwärts verfolgt, werden nur die magentafarbenen Infizierten entdeckt (die dann sofort in Quarantäne müssen). Nur wenn man das Superspreading-Event identifiziert, kann man die gelb markierten Infizierten finden.

Eine Nebenbemerkung zum infektiösen Interval bei SARS-CoV-2: Ursprünglich ging man davon aus, dass Infizierte erst 2 Tage vor Beginn ihrer Symptome ansteckend sind. Das basierte auf einem Fehler in der Datenanalyse in einem einflussreichen frühen Nature-Artikel chinesischer Autoren. Die neue Analyse der Rohdaten durch die ETH Zürich zeigte, dass man 3 Tage vor Symptombeginn nach Kontakten schauen muss, um 80% der Infektionen zu finden, und sogar 4 Tage vor Symptombeginn, um 91% der Infektionen zu finden (siehe Tabelle 2 im Artikel). Dagegen war man vorher davon ausgegangen, dass man 98% der Infektionen findet, wenn man nur bis zu 2 Tage vor Symptombeginn danach sucht. Hier der entscheidende Satz der Schweizer Autoren:
„Our reanalysis suggests that tracing contacts of infected index cases as far back as 2 or 3 days before symptom onset in the index case might not be sufficient to find all secondary cases.“ (Fettdruck nicht im Orginal).

Die Autoren des Orginalartikels in Nature-Medicine haben übrigens in der Folge eine Korrektur veröffentlicht. Die entscheidende Korrektur dabei ist: ‚The time frame in the first sentence of the tenth paragraph of the main body of the text (“2 to 3 days”) was incorrect. The correct time frame is “5 to 6 days.”‚

Allerdings: Offenbar hat das Robert-Koch-Institut seine Kontaktverfolgungsstrategie nicht angepasst, obwohl der Fehler im Nature-Artikel schon seit August bekannt ist (RKI: Kontaktpersonen-Nachverfolgung bei Infektionen durch SARS-CoV-2, Stand: 19.10.2020):
„Unseren Empfehlungen liegen folgende Annahmen zugrunde:

• Die Dauer der Inkubationszeit beträgt in den meisten Fällen maximal 14 Tage.
• Der Mittelwert/Median für die Inkubationszeit liegt bei 5-6 Tagen.
• Die Dauer der infektiösen Periode beträgt etwa 12 Tage. Sie beginnt bei
  • asymptomatischem Quellfall (Exposition bekannt): am Tag 3 nach Exposition;
  • bei asymptomatischem Quellfall (nur Probenahme-Termin bekannt): am Tag 2 vor der Probenahme;
  • bei symptomatischem Quellfall: 2 Tage vor Symptombeginn“ (Fettdruck nicht im Orginal)

und damit konsistent bemisst das RKI das infektiöse Zeitintervall für die Kontaktverfolgung wie folgt:

„Das infektiöse Zeitintervall für symptomatische Fälle mit bekanntem Symptombeginn:
Ab dem 2. Tag vor Auftreten der ersten Symptome des Falles bis mindestens 10 Tage nach Symptombeginn, bei schwerer oder andauernder Symptomatik ggf. auch länger, siehe www.rki.de/covid-19-entlassungskriterien„.

Nach der Analyse der ETH kann man mit der immer noch aktuellen Strategie des RKI nur 61% (Konfidenzinterval 40–83%) finden, die restlichen 39% der Infektionen bleiben unauffindbar.

Noch eine Bemerkung: Aus den Medienberichten ist nicht klar, ob das RKI und die Gesundheitsämter eine Rückwärtsverfolgung wie oben beschrieben betreiben. Es ist aber klar, dass die Gesundheitsämter in Deutschland offenbar eine Form der Rückwärtsverfolgung praktizieren, denn das RKI präsentierte zuletzt die häufigsten SARS-CoV-2-Ansteckungsorte. Die Graphik findet sich auch im Situationsbericht vom 20.10.2020. Allerdings konnten die Gesundheitsämter nur bei 27 Prozent der Infektionen eine Zuordnung zu einem Ausbruchsgeschehen vornehmen: „Insgesamt wurden 55.141 (27 %) von 202.225 übermittelten Fällen mindestens einem Ausbruchsgeschehen zugeordnet. Der Anteil von Fällen, die einem Ausbruch zugeordnet wurden, liegt bei Kindern bei rund 40 %, nimmt dann bei Jugendlichen und jungen Erwachsenen ab und erst in der Altersgruppe der ab 80-Jährigen wieder deutlich zu.“

Leider sind die Daten des RKI zu Ausbrüchen sehr start aggregiert. Der Allgemeinheit wäre durch anekdotische Fallbeispiele (case studies) für vergangene SARS-CoV-2-Übertragungen sicher besser gedient. Daraus könnte jeder Rezepte für sein eigenes Verhalten ableiten. Die Details im  Epidemiologisches Bulletin des RKI vom 17. September sind dennoch interessant. Es handelt sich im die Daten zu den Ansteckungsorten von 55151 Infizierten in Deutschland (allerdings konnte der Ansteckungsort von 147084 Infizierten nicht aufgeklärt werden):

Zu einigen dieser Details: Das RKI berichtet von einer durchschnittlichen Ausbruchsgröße von 4,8 Personen in Schulen (31 Ausbrüche mit 150 Ansteckungen, siehe Tabelle 2) und 5,1 Personen in Kindergärten (33 Ausbrüche, die zu 168 Neuinfizierten führten). Kam es in einem Restaurant zu einem Ausbruch, so wurden 7,2 Personen angesteckt (man wüsste gerne, wie viele Ausbrüche davon geschlossene Gesellschaften waren). Kam es in einem Heim zu einem Ausbruch, wurden mehr als 18 Personen angesteckt. Geschah ein Ausbruch in einem Krankenhaus, dann wurden durchschnittlich mehr als 10 Personen infiziert. Die meisten Ausbrüche (3902) geschahen allerdings naturgemäß im privaten Haushalt; da Haushalte in Deutschland nicht so groß sind, wurden dabei aber durchschnittlich nur 3,2 Personen angesteckt. An Universitäten fand das RKI übrigens nur einen einzigen Ausbruch (mit 4 Infizierten) im betrachteten Zeitraum. Kein Wunder, denn es sind (wenig beachtet durch die Medien) alle Universitäten seit April im fast vollständig virtuellen Modus (E-Learning statt Hörsäle). Und das geht im aktuellen Wintersemester 2020 auch so weiter.

 

Hier noch ein Nachtrag zu SEIR-Modellen:

Ich wurde darauf hingewiesen, dass die diskretisierte Form des SEIR-Modells einfacher zu verstehen ist. In der Tat wollte ich schon seit Langem den Octave-Quellcode hier besprechen. Allerdings kam ich nie dazu.

Hier daher die Iterationsvorschrift (entnommen aus der Octave/Matlab-Implementierung), die bei Diskretisierung mit dem expliziten Euler-Verfahren herauskommt (hier Schrittweite 1 Tag):

t=[1:n];
for i=t
  S(i+1)=S(i)-beta*S(i)*I(i);
  E(i+1)=E(i)+beta*S(i)*I(i)-alpha*E(i);
  I(i+1)=I(i)+alpha*E(i)-gamma*I(i);
  R(i+1)=R(i)+gamma*I(i);
endfor

Dabei sind S die Infizierbaren (susceptibles), E die Exponierten (exposed),  I die Infizierten (infected), und R die Geheilten oder Verstorbenen (recovered/removed). Alle diese Variablen nehmen Werte zwischen 0 (0 Prozent) bis 1 (100 Prozent) an.

Für die Parameter gilt: 1/alpha ist die Zeit in Tagen, in der “exponiert” zu “infiziert” wird (Latenzzeit), 1/beta die Zeit zwischen zwei Kontakten in Tagen, 1/gamma die infektiöse Zeit in Tagen.

Sinnvolle Werte können etwa sein:

alpha = 1/3;
gamma = 1/10;
beta = R0*gamma;

bevoelkerung=82000000;

Und als Start für die Infizierten istart=1000/bevoelkerung.

Natürlich kann man das Verfahren auch in jeder Tabellenkalkulation implementieren. Die Schrittweite von einem Tag ist zwar etwas ungenau, wenn man über viele Tage rechnet, aber es geht ja nicht um tagesgenaue Vorhersagen.

Hier die Übungsaufgabe aus dem Sommersemester aus der Veranstaltung Numerik für Mathematiker/innen. Diese Aufgaben könnte sogar in einer Tabellenkalkulation gelöst werden (aktuelles R: zwischen 1,2 und 1,4)